一个小学校长最近谈到她与家长之间关于三年级数学课程的一些谈话。家长觉得教师应该大力强调背诵乘法表。家长认为，三年级的数学应该包括通过机械记忆和练习、工作表以及其他手段来帮助记忆乘法算式。但这位校长正在提倡一种鼓励问题解决和理解的教学方法。她向家长解释，这种方法会帮助学生将乘法过程记忆保留得更长久。她通过自己的经验解释，那些在三年级掌握了乘法表的学生在以后的日子里几乎都不再记得。显然，三年级记忆的乘法表并没有什么作用，因为乘法表并没有帮助学生建立对乘法概念的理解。即使经过“回到基础（back to basics）”和课程的学习。他们仍然不知道乘法为何物。

《学校数学教学原则与标准》（NCTM，2000）指出，“在理解的基础上学习数学是根本”。研究显示，“事实性知识、过程熟练性和概念理解的三者结合将使这三个成分发挥更有效力的作用”。NCTM的《课程焦点》（NCTM，2006）强调“学生通过演示的方式理解整数乘法和除法的意义”。

通常，学生很自然地发展了加法能力，但乘法比加法复杂得多，因此需要通过指导才能理解每个步骤都是组成整个运算过程的重要成分。在尚未获得对于乘法的理解之前记忆算式，学生会对理解乘法意义的需求和适用乘法的情境产生错误印象。

因此，理解乘法意味着什么呢？数学教育文献指出，对于乘法的基本理解需要四个相互关联的概念：（1）数量；（2）需要用到乘法的问题情境；（3）相等的组；（4）与乘法有关的单位。在低年级，大多数理解是通过儿童数数和分组策略在解决有意义问题的经验中获得的。

●理解数量。在加法中，数量的意义常常被忽略，然而，这是理解乘法的重要基础。数量是物体能够被计数和被测量的种特性，它包括一个数字和一个单位。7美元就是数量的一个例子，它包含了数字7和单位“美元”。数词（例如，7）通常用来表示数量的数的部分，当然数也可以用其他的方式表示，比如图片（如，可以用7张钞票表示7美元）。除了数字之外，必须要确定一个单位才能获得完整的数量概念。一个计数是数的一种特别类型，属于多个物体组成的集合的数量特征的一部分，它用来回答“多少”的问题。数数是从一个一个数开始，然后发展到数更大的相同单位的数。学生需要积累大量的数数经验，才能清楚地知道数量的这两个属性以及多种表示方法。而测量（如，长度）也是数的一种特殊类型，它是关于一个物体的连续特性。测量包括选择测量的合适单位（如，英寸），并确定在这个物体的连续特性方面所包含的单位的数目。因此，为了全面了解数量，学生需要了解离散量与连续量之间的区别，认识到它们是用不同的单位和不同的步骤（数数VS.测量）来确定数量的值的。

●理解需要用到乘法的问题情境。学生需要一定的经验来解读需要用到乘法的文字应用题情境，并与其他需要运用加法、减法或除法的情境区分开。学生还需要理解乘法与除法之间的关系，并能够根据算式的三个数中已知的任何两个数的信息，得出另未知数（如，3X7=？或3X？=21）。

●理解相等的组。学生需要练习将物体分组，以理解乘法中相等组别的作用，并理解等组相乘而不是将所有物体相加所带来的效率。数感包括将数字组合和拆分的能力。乘法中的推理包括在组合和拆分数字时，用因数和倍数均分等组，而不是相加。例如，8个物体可以分成各种表示乘法的组（8个一组，4个一组的2组，2个一组的4组或者一个1组的8组）而不是表示加法的组（1和7，2和6，4和4，8和0）。视觉图像对于理解分组尤其有用（如，60件散乱的物品和被分成12个一组的5组物品，或排成一列6个共10列的60件物品之间的差别）。

●理解与乘法相关的单位。学生需要练习将物体分组并数数，才能理解与乘法有关的各种单位之间的差异。加法最常涉及的是将相同单位不同数量组合的情境（如，35分钱加24分钱）。然而，乘法中的两个数量还常常具有不同的单位（如，每条狗的4条腿乘以12条狗）。学生还需要理解单位在乘法中可能发生的转换。例如，7个橙子加7个橙子得到的是14个橙子，但是两个相同的单位相乘，例如7英寸乘以3英寸，却得到21平方英寸。

一种加深学生对乘法过程理解的办法是用手算演示乘法的不同运算方法。图5.8展示了将一个三位数与一个两位数相乘所采用的传统方法（a），以及被称为方格乘法的方法（b）。乘法需要三步：相乘、进位和相加。在传统方法里，相乘和进位步骤是一起做的，所以很容易混淆。在方格乘法中，每一步都很清晰。这个方法是由著名的数学家斐波那契（Fibonacci）于1202年通过他的专著《计算之书》（Liber Abacii）引人欧洲的。 

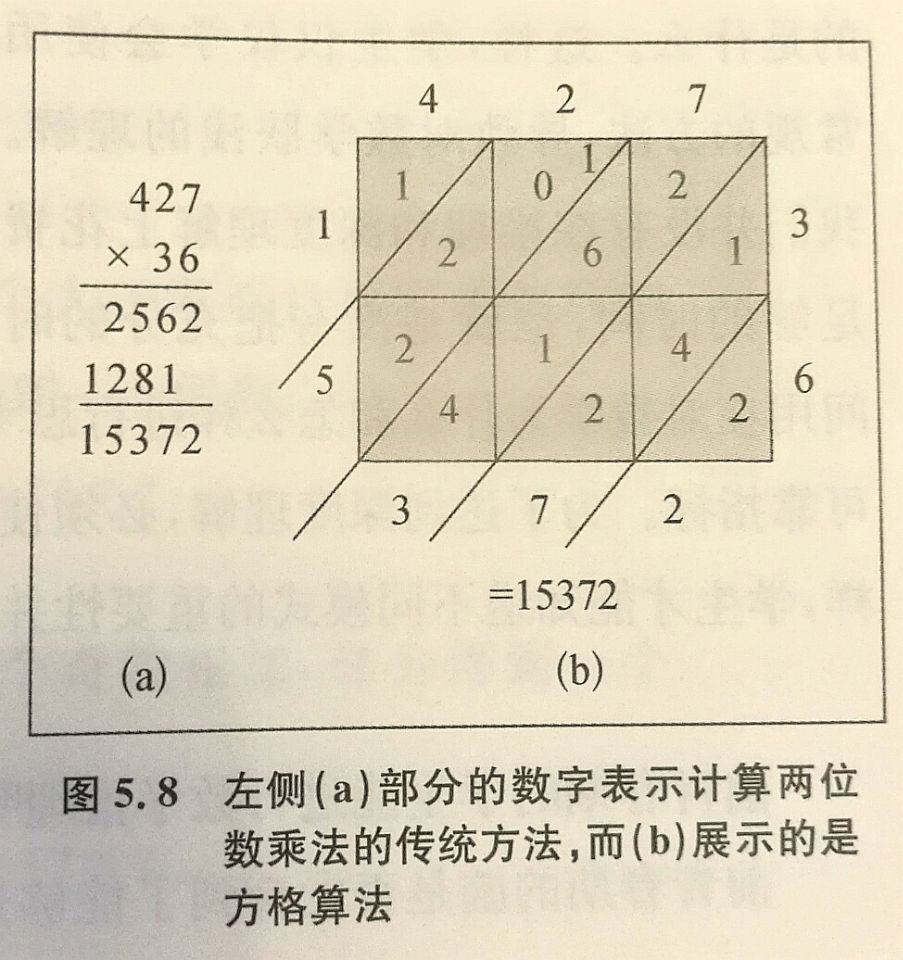
步骤很简单。如果我们要将427乘以36，则将427写在格子的上方，将36竖着写在一个3X2的矩形方格（因为我们有一个三位数和一个两位数）的右边。我们将上方横排的数字与每一行右侧的数字相乘并填人格中，如果得数为两位数，那么将十位上的数字写在每个方格的对角线的上方，而个位数写到对角线的下方；如果得数是一位数，那么在对角线上方填入零，而将个位数写到对角线下方。

当所有的组合都乘完后，我们顺着对角线将数字相加，从对角线内右上方的数字开始，然后沿对角线相加并将所得的和放到格子的左外侧；如果得数是两位数，那么将十位数放到对角线左侧的最上一行，并且加入到那列对角线的得数中。从格子外侧的左上方起，将所得数字一直读到底部，这样得到答案15372。这个方法不是万能的，但它能提供新颖的也许是一些学生所需要的能更好理解乘法步骤的方法。

本文内容转载自《人脑如何学数学》一书，如存在版权问题请及时联系我们，我们坚持保护原创者的知识版权。